Основные геометрические фигуры с названиями и описанием

Во всех окружающих предметах просматриваются геометрические фигуры. Все их многообразие сводится к нескольким основным, которые систематизирует геометрия. Какие это фигуры, чем они характеризуются?

Какие основные геометрические фигуры? Сайт Libre Texs Mathematics относит к основным геометрическим фигурам точку, прямую линию (отрезок и луч), кривую и ломаную линии, в том числе все виды многоугольников, а также окружность.

Точка

Что такое геометрические фигуры? Это совокупность такого множества точек, линий или тел, которые расположены на плоскости, поверхности или в пространстве и образуют конечное число линий. В повседневной жизни геометрические фигуры — это образ реального предмета, в котором сохраняется только форма и размеры, и только они принимаются во внимание.

Самая малая геометрическая фигура — это точка. Она не имеет измерительных особенностей и характеристик: не содержит длины, высоты, объёма, площади. Как пишет платформа Libre Texs Mathematics, это просто местоположение на плоскости.

Но самая малая геометрическая форма точка — самая главная, ведь она необходима для построения других фигур и всегда будет их основой. В геометрии точка обозначается заглавными буквами латинского алфавита A, B, C, D и т. д. Чтобы нарисовать точку, нужно только прикоснуться карандашом к бумаге.

Через одну точку можно провести бесконечное число линий. Через две точки можно провести только одну линию.

Прямая линия

Линия — фигура, которая состоит из множества соединенных между собой точек, расположенных последовательно друг за другом на прямой.

Линии бывают прямыми, кривыми и ломаными. Прямые линии не имеют начала и конца, они бесконечны. На листе бумаги можно увидеть лишь часть прямой линии, так как она не имеет пределов. С прямой линией связаны другие геометрические фигуры:

Отрезок — часть прямой линии, ограниченная с двух сторон точками.
Луч — направленная полупрямая, у которой есть точка начала, но нет конца.

Если на прямой поставить одну точку, она разбивает линию на два противоположно направленных дополнительных луча. Если на прямой поставить две точки, они разобьют её на отрезок в середине и два луча по краям.

Кривая линия

К точному и единому определению кривой линии математики не пришли. Чаще под кривой линией подразумевают непрерывное одномерное множество точек, которые отвечают условиям этой кривой. Кривые линии могут изгибаться в зависимости от вида заданной фигуры.

Нарисовать кривую линию можно без линейки, достаточно воображения. Множество кривых линий отличаются огромным разнообразием. Самые известные и простые кривые имеют волнообразную форму.

Самостоятельно такую линию можно провести так: обозначить на плоскости две точки на любом расстоянии. Из первой точки вести линию не по прямой к другой точке, а по любой траектории, например, подняться по дуге вверх и опуститься вниз, чтобы соединить линию со второй точкой.

Ломаная линия

Ломаная линия — это несколько отрезков, соединенных так, что конец первого отрезка становится началом второго, конец второго — началом третьего и т. д. При этом соседние отрезки располагаются на разных прямых.

Все точки ломаной линии, в которых соприкасаются отрезки, называются вершинами. Их в геометрии тоже обозначают заглавными латинскими буквами.

Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой. Если они совпадают, то создают замкнутую ломаную линию. Всякий многоугольник представляет собой такую замкнутую ломаную линию. Самые известные из них — это треугольники и четырёхугольники во всем разнообразии.

Замкнутая линия делит плоскость на внутреннюю и внешнюю области. При этом образованные фигуры имеют такие характеристики, как периметр и площадь:

Периметр — это сумма длины всех отрезков замкнутой ломаной линии. Измеряется он в единицах длины (мм, см, м, км). Обозначают периметр латинской буквой Р.
Площадь геометрической фигуры — это занимаемое ею место на плоскости. Измеряется в мм², см², м², км². Площадь обозначается латинской буквой S.

Вычисляют периметр и площадь с помощью специальных формул. Существуют формулы для треугольников, четырёхугольников, окружностей, кругов.

Треугольники

Треугольник — это геометрическая фигура, созданная замкнутой ломаной линией из трёх звеньев (отрезков). Эти три отрезка соединяются в трёх точках, которые не лежат на одной прямой. Точки соединения называются вершинами треугольника (обозначаются заглавными латинскими буквами), отрезки — его сторонами.

Треугольники бывают нескольких видов. По углам они делятся на такие виды:

Прямоугольные, если один угол прямой.
Остроугольные, когда градус всех его углов больше 0, но меньше 90.
Тупоугольные, если один угол тупой (больше 90°), а два других — острые.

По сторонам треугольники бывают такими:

Равнобедренные, если две стороны равны.
Равносторонние, если все стороны одинаковы по длине.
Со сторонами различной длины.

Особенности разных треугольников изучает геометрия. Для них существуют особые правила и характеристики, например, сумма углов треугольников всегда составляет 180°.

Четырёхугольники

Четырёхугольники создаются замкнутой ломаной линией из четырёх звеньев (отрезков). В геометрии они представлены такими геометрическими фигурами:

Прямоугольники, которые состоят из четырёх сторон и четырёх прямых углов.
Квадраты, у которых равны все стороны, а все углы составляют 90°.
Параллелограммы, у которых противоположные стороны попарно параллельны.
Ромбы, которые представляют собой параллелограмм с равными сторонами. При этом противоположные стороны и углы равны.
Трапеции — четырёхугольники, у которых две стороны параллельны (называются основаниями), а две — разные. Трапеции бывают равнобокими (боковые стороны равны), прямоугольными (одна из боковых сторон перпендикулярна основаниям).

Четырёхугольники отличаются особыми свойствами. Так, сумма их углов равна 360°, и нет четырёхугольников, у которых все углы острые или все тупые.

Окружности

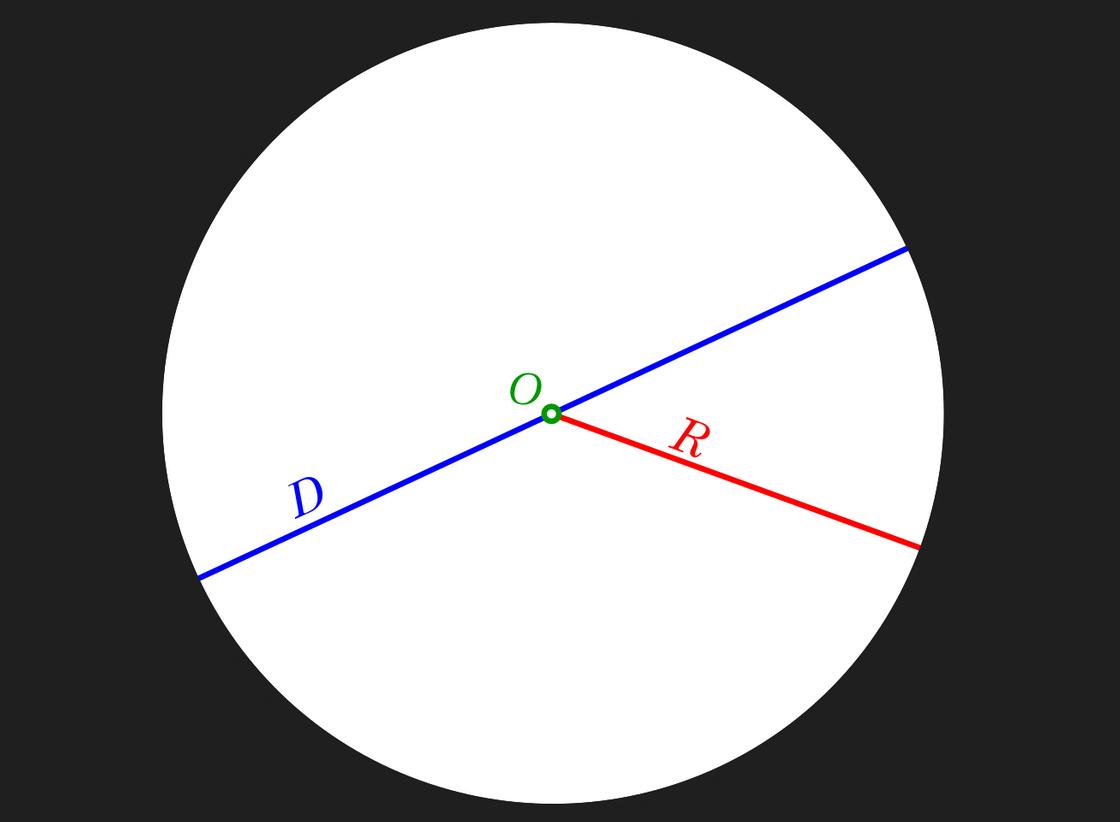
Окружность — это геометрическая фигура, которую создает замкнутая кривая линия, а все её точки находятся на одинаковом расстоянии от центра. Часть плоскости внутри окружности известна как круг. Окружность ещё называют границей круга.

У окружности есть:

Радиус — это расстояние от центра до любой точки окружности.
Диаметр, который соединяет две точки на окружности и проходит через её центр. Диаметр равен двум радиусам.
Хорда — отрезок, соединяющий любые две точки на окружности.
Дуга — часть окружности между двумя её точками.

Старшеклассники изучают специальные формулы, по которым вычисляется длина окружности и площадь круга.

Многие педагоги уверены, что дети 6–7 лет должны овладеть базовыми представлениями о геометрических фигурах. Это непременное условие для формирования математического склада ума. Специалисты дошкольного образования утверждают, что именно в детском возрасте складывается правильное понимание формы геометрических фигур, что потребуется в учебе и повседневной жизни.

Основные геометрические формы встречаются во всех предметах и в природе. Поэтому они имеют важное значение в познании детьми окружающего мира.